一、概览

这篇文章的内容主要基于Olsson & Hibbs 2005年的理论展开，该理论建立了一套简单模型来描述13000年前到现在的经济发展，以11000BC的地理和生物条件出发描绘了人类冲出马尔萨斯陷阱的前后。Olsson & Hibbs选取四个地理标准（Climate, Latitude, Axis, Size）和两个生物标准（Animal, Plants适于驯化及养殖的种类多少），通过一系列的实证研究，用11000BC的地理生物环境跑回归模拟了1997年国家人均GDP排序，成功模拟了100个国家中半数的GDP排序（考虑到年代跨越巨大，模型变量很少，这个成果十分令人惊讶）。

Enlarge

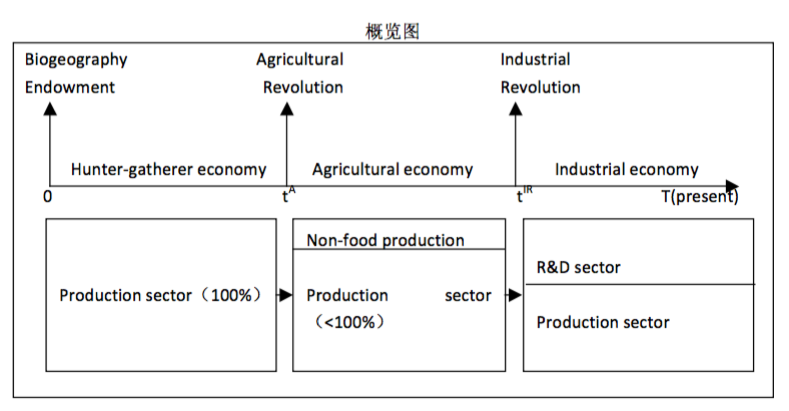
用这张图和一句话可以概括Olsson & Hibbs的理论：自然禀赋的不同使得各地区适合人类居住的程度不同，在易于定居的地方逐渐形成了固定农业，一开始所有人都在从事农业，在农业革命之后，由于技术进步一部分人从农业中释放出来形成non-food class，从事社会管理及科技发展，最终工业革命之后的技术进步促使一个地区逃离马尔萨斯陷阱。

这里我们想问的问题是：自然禀赋的哪些特征最重要？在自然禀赋高的地方真的最先开始农业革命么？这些自然禀赋是怎样影响人类行为的？这些影响带来的地区差异持续至今天么？这篇文章会针对这几个问题对Olsson & Hibbs模型进行阐述。

二、从自然禀赋到农业革命

生物条件还未成型之前，地理条件率先成型，形成包括Climate, Latitude, Axis, Size在内的一组地理参数，这一组地理参数形成了不同的适合生物生存成长的条件，从而决定了一个地区内的适合于农业的Animal, Plants种类及多少 。

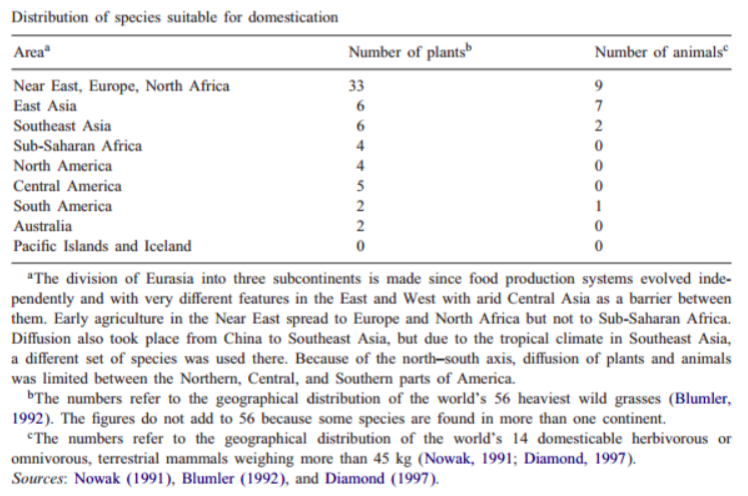
这张图表显示了早期各个地区适宜种植的植物种类和适于驯养的动物种类：

Enlarge

根据Blumler（1992）的研究，全球共有56种植物适合农业种植需要，14种哺乳动物适合驯养需要。要形成稳定的固定农业，一个地区至少需要两种以上适合种植的植物及至少一种适合驯养的动物。上表所剩只有四个地区符合条件，Near East, Europe, North Africa的自然禀赋最为突出，East Asia和Southeast Asia也不错。

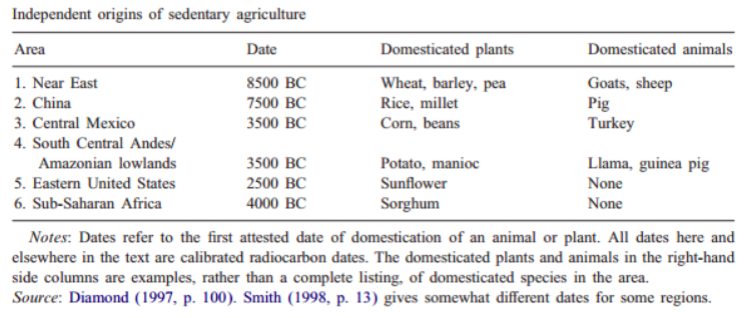
这张表是各个地区各自产生固定农业的时间：

Enlarge

不算完美匹配，但是大致符合。

三、从农业革命到工业革命

按照Olsson & Hibbs模型来看，这一部分更像是一个概念模型，它依然处于马尔萨斯陷阱之中，但是人类不再单纯从事生产。在自然禀赋优越的地区农业发展较快（具体的model后面会给出），农业生产力的提高使得一部分的人空余出来，从事一些非农业的活动，如写字、文化创造、科学研究、社会事务、公共管理。在这个时期，人口与技术之间的马尔萨斯关系还存在，也就是，技术的进步依然比较慢，其最终的结果也还是人口增加，经济依然没有显著的增长。但是文化与社会管理以及技术的积累，科技的重要性也在人类社会中得到重视，教育开支也逐渐加大（这个model会在第三篇children quality & children quantity 描述），与技术发展形成了相互促进的局面，工业革命随之爆发。

四、工业革命

最早产生于18世纪英国的工业革命彻底撕碎了人口与技术之间的马尔萨斯关系。工业革命之后的地区人口不再跟随技术按比例增长，出现了现代经济中所谓的内生增长。这个部分Olsson & Hibbs没有过多的工作，现代经济理论已经有很多相关研究，他们跑了一个回归，用他们的模型来验证11000BC的自然禀赋函数与1997人均GDP的关联，下一节会简单讨论。

五、Olsson & Hibbs model

产出模型（ From Romer Model,1990）：

\(Y_n(t)=\frac{\delta (t)A_n(t)(v(t)L_n(t))^{1-\alpha}}{L_n(t)} \) (1)

• \(δ(t)>=1\) : The level of productivity
• \(A_n(t)>0\) : state of technology or knowledge
• \(V(t)\) : the fraction of total population engaged in food production
• \(L_n(t)\) : total population
• \(α∈(0,1)\) : output elasticity of capital

1. Hunter-gatherer economy

此时的条件为：

• \(y_n(t)=y\) （人均产出固定）
• \(δ(t)=1\)
• \(A_n(t)∈[1,A_n]\)     A_n表示一个地区的最大资源禀赋，A_n为被驯化的动植物
• \(v(t)=1\)

此时可得\(y=A_n(t)L_n(t)^{-\alpha}\)

Olsson & Hibbs再直接假设： \(\frac{A_n^{t+1}-A_n^t}{A_n^t}=\gamma A_n\)  (2)，γ为一个常量

也就是，技术进步的速度直接取决于一个地区的最大资源禀赋，这一点的解释是，一个地区禀赋越高，人就有更大的概率得到禀赋

可以进一步得到：\(A_n(t)=A(0)exp(\gamma A_nt) = exp(\gamma A_nt)\)  (3)  (假设A(0)=1)

达到农业革命时，已驯化的动植物量为A^A，对一个地区来说，如果A_n<A^A, 这个地区不可能发生农业革命，因为A_n(t)函数最大上限为A_n<A^A，就像澳洲，只有当一个地区A_n>A^A, 才有农业革命的潜在可能。

对（3）取对数：\(t_n^A=\frac{lnA^A}{\gamma A_n}=\frac{\kappa}{A_n} \) \(\kappa>0\) 常数

模型到这个地方的意义是，t_n^A代表到达农业革命的时间，其只与A_n有关，也就是说自然禀赋越高的地方越快发生农业革命（T- t_n^A表示农业革命之后的时间，使其对A_n求偏导，一阶大于零二阶小于零，为递增凸函数，也就是说，禀赋越高越快进行农业革命，但是禀赋增加对时间减少的回报是递减的）。

通过实证研究，此阶段y增长率为零，而要使得其为零，只需假设：

\(\frac{L_n^{t+1}-L_n}{L_n}=\frac{1}{\alpha}\frac{A_n^{t+1}-A_n}{A_n}=\frac{\gamma A_n}{\alpha}\)(4)

2. Agricultural economy

此时的条件为：

• \(y_n(t)=y\) （人均产出固定）
• \(δ(t)= δ^A>1\)
• \(A_n(t)>A^A\)
• \(v(t)=v^A<1\)

可以得到：\(\frac{A_n^{t+1}-A_n}{A_n}=1-v^A>0\)

假设(4)\(\frac{L_n^{t+1}-L_n}{L_n}=\frac{1}{\alpha}\frac{A_n^{t+1}-A_n}{A_n}=\frac{\gamma A_n}{\alpha}\)依然成立，

所以y的增长率为\(\frac{y_n^{t+1}-y_n}{y_n}=\frac{A_n^{t+1}-A_n}{A_n}-\alpha\frac{L_n^{t+1}-L_n}{L_n}=0\) 也依然成立。

这个部分模型似乎没有太大意义…

3. Industrial economy

此时的条件为：

• \(y_n(t)>y\)  (y开始变化了)
• \(δ(t)= δ^{IR}>δ^A>1\)
• \(A_n(t)>A^{IR}\)
• \(v(t)=v^A<1\)

此时，模型的本质区别在于y的增长率变了，因为假设(4)\(\frac{L_n^{t+1}-L_n}{L_n}=\frac{1}{\alpha}\frac{A_n^{t+1}-A_n}{A_n}=\frac{\gamma A_n}{\alpha}\)没有了，人口增长不再是技术增长的函数，而是常数η。

科技进步率与从事R & D的人数成比例，也就是\(\frac{A_n^{t+1}-A_n}{A_n}=1-v^{IR}\)

所以此时y的增长率为\(\frac{y_n^{t+1}-y_n}{y_n}=\frac{A_n^{t+1}-A_n}{A_n}-\alpha\frac{L_n^{t+1}-L_n}{L_n}=1-v^{IR}-\alpha η > 0\) (5)

αη为常数，所以的增长与科技进步率1-v^IR直接相关。

4. Comparative statics

(5)转化可以得到：\( lny_n(T)=lny+(1-v^{IR}-\alpha \eta )(T-0-\frac{\kappa}{A_n})\)

lny_n(T) 代表现在的人均GDP的log值，其对A_n求偏导一阶为正二阶为负，为关于A_n的凸函数。Olsson & Hibbs最后跑的回归模型就是用这个函数得来，数据序列和更多细节可以到两位的网站去找：

http://www.handels.gu.se/econ/Macroeconomics/rpubs.html

六、关于Olsson & Hibbs模型（个人观点，站着说话不腰疼系列）

1. Olsson & Hibbs模型的视角很新鲜，有一种从自然的角度出发，以自然资源为内生变量，将人类社会发展设定为外生变量的“上帝”视角的感觉，阐述人类经济的客观发展逻辑。
2. 揭示了早期地理、生物资源与人类发展强相关的逻辑。
3. 模型中缺乏对诸如假设(4)的有效解释（直接通过客观事实规定了这个假设），而这个缺口抹杀了模型的动态，整个模型因而是一个不连续的静态模型。
4. 模型的阶段性分类似乎也欠缺强逻辑性，阶段2，agricultural economy，感觉没有很强的特殊性需要单独列为一个阶段（难道是为了让文章看起来更充实或者骗稿费？），它的假设跟阶段一很相似，同时过程也很相似，没有经济增长。反观阶段一，如果人类群落存在，就不可能全部人的全部时间都投入食物生产，即，如果把阶段一列为一个逻辑上的概念起点，而阶段二作为马尔萨斯阶段的发展过程，可能更为合理。
5. 这个理论的第二阶段的起点可能有一点含糊，有一点像从农业革命开始，但是仔细思考似乎跟从固定农业开始区别不大有点混淆，理论中没有阐明固定农业和农业革命的关系。
6. 如果群落在第二阶段农业阶段，他们是怎么突变到工业阶段的？动态的缺乏使得这个模型似乎没有解释阶段二中技术积累的量变过程，从而第三阶段的质变不是由二阶段量变得到而是重新起假设得到。
7. 抛开从模型的观点看，这个理论是一个很好的add to thinking。